基本计数方法

求和

$ans=\sum_{i=1}^n a_i$

int ans=0;for(int i=1;i<=n;i++) ans+=a[i];

求积

$ans=\prod_{i=1}^n a_i$

int ans=1;for(int i=1;i<=n;i++) ans*=a[i];

阶乘

$n! = 1 \times 2 \times L \times (n-1) \times n$

int ans=1;for(int i=1;i<=n;i++) ans*=i;

排列

$A_n^k = \frac{n!}{(n-k)!}$

int ans=1;for(int i=n-k+1;i<=n;i++) ans*=i;

组合

$C_n^k = \frac{n!}{k!(n-k)!}=\frac{A_n^k}{k!}$
$C_n^k = C_n^{n-k}$

ll fp(ll a,ll b)
{
	ll ret=1;
	while(b)
	{
		if(b&1) ret=ret*a%p;
		b>>=1;
		a=a*a%p;
	}
	return ret;
}
ll C(int n,int m)
{
	if(m>n) return 0;
	ll ret=1;
	for(int i=1;i<=m;i++)//from n to (n-m+1)
	{
		ll a=(n+i-m)%p;
		ll b=i%p;
		ret=ret*(a*fp(b,p-2)%p)%p;
	}
	return ret;
}

容斥原理

$|A_1 \cup A_2 …… \cup A_m| = \sum_{1 \leq i \leq m} |A_i| - \sum_{1 \leq i,j \leq m} |A_i \cap A_j| + …… + (-1)^{m-1}|A_1 \cap A_2 \cap …… \cap A_m| $

Lucas定理

对于非负整数m和n和素数p， 同余式:

${\binom {m}{n}} \equiv \prod_{i=0}^{k}{\binom {m_{i}}{n_{i}}}{\pmod {p}}$

成立。其中：

$m=m_{k}p^{k}+m_{k-1}p^{k-1}+\cdots +m_{1}p+m_{0}$

并且

$n=n_{k}p^{k}+n_{k-1}p^{k-1}+\cdots +n_{1}p+n_{0}$

是m和n的p进制展开。当m < n时，二项式系数 ${\binom {m}{n}=0}$。

二项式系数 可被素数 p 整除当且仅当在p进制表达下n的某一位的数值大于m对应位的数值。

$C_n^m \% p = C_{n \% p}^{m \% p} \times C_{n / p}^{m / p} \% p$
代码实现:(fzuoj2020)

//C(n,m)%p Lucas spaceskynet 08-21
#include<cstdio>
typedef long long ll;
int n,m,p;
ll fp(ll,ll);
ll C(int,int);
ll Lucas(int,int);
int main()
{
	int t;
	scanf("%d",&t);
	while(t--)
	{
		scanf("%d%d%d",&n,&m,&p);
		printf("%lld\n",Lucas(n,m));
	}
	return 0;
}
ll fp(ll a,ll b)
{
	ll ret=1;
	while(b)
	{
		if(b&1) ret=ret*a%p;
		b>>=1;
		a=a*a%p;
	}
	return ret;
}
ll C(int n,int m)
{
	if(m>n) return 0;
	ll ret=1;
	for(int i=1;i<=m;i++)//from n to (n-m+1)
	{
		ll a=(n+i-m)%p;
		ll b=i%p;
		ret=ret*(a*fp(b,p-2)%p)%p;
	}
	return ret;
}
ll Lucas(int n,int m)
{
	if(m==0) return 1;
	else return C(n%p,m%p)*Lucas(n/p,m/p)%p;
}

二项式定理

$(a+b)^n = \sum_{r=0}^n C_n^r a^{n-r}b^r$

展开项系数和为$2^n$

$2^n = (1+1)^n = C_n^1+C_n^2+……+C_n^{n-1}+C_n^n$

从左上角走到右下角的最短路径有多少条?

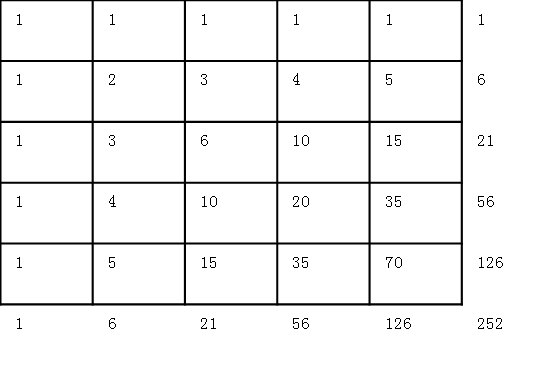
旋转45°：（杨辉三角）

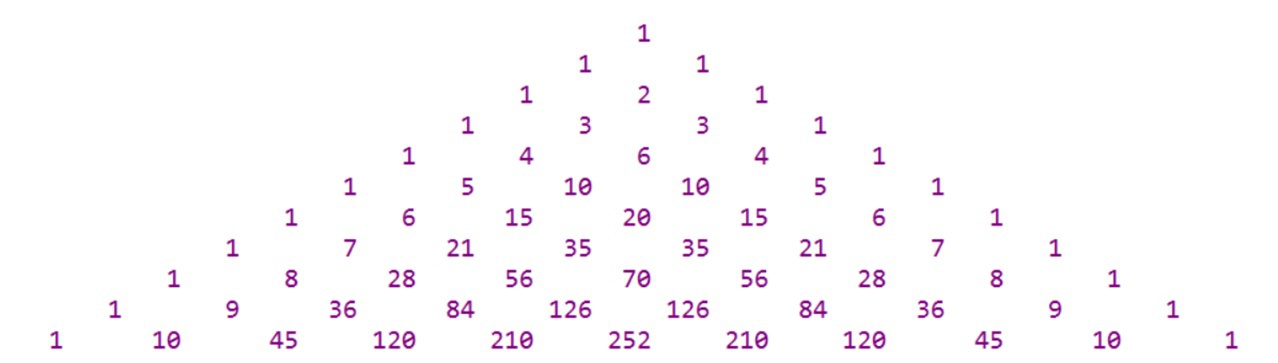
可得出：
$C_n^m = C_{n-1}^m + C_{n-1}^{m-1}$

const int maxn=1e3+10,mod=1e9+7;
for(int i=0; i<=maxn; i++)
{
	for(int j=0; j<=i; j++)
	{
		if(j==0) C[i][j]=1;
		else C[i][j]=(C[i-1][j-1]+C[i-1][j])%mod;
	}
}

质数

判断质数

一个不被所有小于等于其算术平方根的质数 整除的数是质数。

Eratosthenes筛法$O(nlog_2n⁡log_2⁡n)$

bool a[101];
memset(a,1,sizeof(a));
a[1]=0;
for(int i=2;i<=sqrt(n);i++)
{
	if(a[i])
	{
		for(int j=2;j<=n/i;j++)
		{
			a[i*j]=false;
		}
	}
}
for(i=2;i<=n;i++)
{
	if(a[i])cout<<i<<" ";
}

线性筛$O(n)$

void createPrime(int n)
{
	for(int i=2;i<n;i++)
	{
		if(!isnotPrime[i])
		{
			prime[numPrime++]=i;
		}
		for(int j=0;i*prime[j]<n&&j<numPrime;j++)
		{
			isnotPrime[i*prime[j]]=1;
			if(!i%prime[j]) break;
		}
	}
}