二分查找用于求单调函数的零点。
而三分查找用于求单峰函数的极值。
速度快，但是结果并非准确值，需自己控制精度。

方法

首先，在函数上标4个点：$x=l,r,mid,mmid$。其中$mmid$是$mid$与$r$的中点。

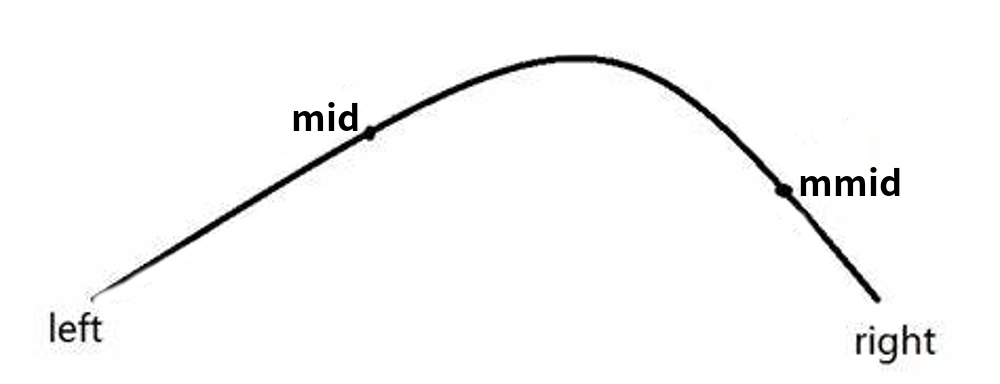
然后通过迭代缩小范围：
对于凸点

1. 如果$f(mid)>f(mmid)$，则$mmid$一定在峰的右边。
2. 如果$f(mid)<f(mmid)$，则$mid$一定在峰的左边。

对于凹点

1. 如果$f(mid)>f(mmid)$，则$mid$一定在峰的左边。
2. 如果$f(mid)<f(mmid)$，则$mmid$一定在峰的右边。

证明：

对于凸点

1. 假设存在$f(mid)>f(mmid)$且$mmid$在峰的左边。
   根据定义（$mmid = \frac{mid+rt}{2}$）显然$mid$在$mmid$的左边。
   然而峰为凸点，左侧单调递增，所以$f(mid) < f(mmid)$。矛盾。
2. 假设存在$f(mid) < f(mmid)$且$mid$在峰的右边。

显然$mmid$在$mid$的右边。
然而凸点右侧单调递减，所以$f(mid)>f(mmid)$。矛盾。
对于凹点
同理可得。

正确的使用方法

首先我们要证明，需要三分的函数是个单峰函数（当然可以da dan cai xiang）。
然后就三分了。

如何控制精度？

两种办法。一种是控制迭代次数，一种是直接控制精度。
控制迭代次数：设一个$dep$值，迭代了$dep$次之后就退出。
直接控制精度：设一个精度限制$eps$，如果$r-l < eps$就退出。
具体用哪种方式由题目决定。
相对精度 —> 控制迭代次数比较好；
绝对精度 —> 控制精确到小数点后多少位比较好。

例题

luogu P3382

题目描述

如题，给出一个N次函数，保证在范围[l,r]内存在一点x，使得[l,x]上单调增，[x,r]上单调减。试求出x的值。

输入输出格式

输入格式：

第一行一次包含一个正整数N和两个实数l、r，含义如题目描述所示。
第二行包含N+1个实数，从高到低依次表示该N次函数各项的系数。

输出格式：

输出为一行，包含一个实数，即为x的值。四舍五入保留5位小数。

输入输出样例

输入样例#1：

3 -0.9981 0.5
1 -3 -3 1

输出样例#1：

-0.41421

说明

时空限制：50ms,128M

数据规模：

对于100%的数据：$7<=N<=13$

Code

#include<cstdio>
typedef double db;
const int maxn=15;
const db eps=1e-6;
int n;
db a[maxn]={0};
db f(db);
int main()
{
	db l,r;
	scanf("%d%lf%lf",&n,&l,&r);
	for(int i=0;i<=n;i++)
	{
		scanf("%lf",&a[i]);//看清系数顺序 
	}
	db mid,mmid;
	while(r-l>eps)
	{
		mid=(l+r)/2,mmid=(mid+r)/2;
		if(f(mid)>f(mmid)) r=mmid;
		else l=mid;
	}
	printf("%.5f",mid);
	return 0;
}
db f(db x)
{
	db ret=a[0];
	for(int i=1;i<=n;i++)
	{
		ret=ret*x+a[i];
	}
	return ret;
}